bay Alignment Systematic by Loft Time
Shoot at where the target will be, not where it is right now
Here we explain the method we followed in our evaluation of the Carolina bays.Our conjecture speculates that the Carolina bays structures are surface features in energetically deposited, highly hydrated, distal ejecta from a cosmic impact. For many decades, maps have been drawn which attempt to identify the source of the Carolina bays by using the inferred long-axis orientation of the various bays as an arrival bearing. Drawn of "flat" maps, those attempts failed to account for the fact that the flight path of any ejecta product would not show up on a projected map as a straight line, but rather be a curve following a great circle route. The underlying concept is a geospatial reference-frame principle called the Coriolis force, or “effect”.
 Image example CorioliskraftanimationCC By Hubi - German Wikipedia CC BY-SA 3.0
Image example CorioliskraftanimationCC By Hubi - German Wikipedia CC BY-SA 3.0Please reference the classic map from the Eyton & Parkhurst paper for an example of flat maps and straight lines.
Google Earth allows for the creation of true great circle lines using the "Insert>New>Path", or by programmatic creation of the appropriate kml. A quick test of paths drawn back from numerous Carolina bays confirms the general trend to the north-west.
Most attempts at following the inferred orientation of the bays back up the trajectories' bearing have failed to produce a focus. We propose this to be caused by at least two variables not considered. First, that the impact may have been a "train-of-craters" event or oblique impact oval crater, which would infer a chaotic focus, and secondly, that the earth rotates during any realistic ejecta loft time. (Systematic by Loft Time) A third variable is the proper accounting for the west-to-east ground-velocity vectors that will be resolved when the ejecta strikes the earth (Systematic by Latitude), but they are measured in meter/sec vs km/sec).
During the time period extending from the moment of the source impact to the eventual deposition of the distal ejecta, we see the de-coupling of the spatial coordinate reference systems in multiple dimensions. The decoupling is driven by the spherical nature of the "playing field" when trajectories cover significant distances. The common term applied to the effect is the Coriolis Force, which is a kinematic force applied to an object to "force" it along a great circle route as a object proceeds along its trajectory. For example, if an object is launched with sufficient velocity on an azimuth of 90 degrees from latitude 45 north (i.e. due East), it will follow a great circle route as it begins to "circle" the earths spherical surface. The cartesian coordinate "bearing" of our example object begins to "turn" south, and eventually the object will cross the equator on an azimuth 45 degrees increased, or 135 degrees. But the above analysis does not account for the fact that the earth is also rotating during any real-world loft trajectory period.
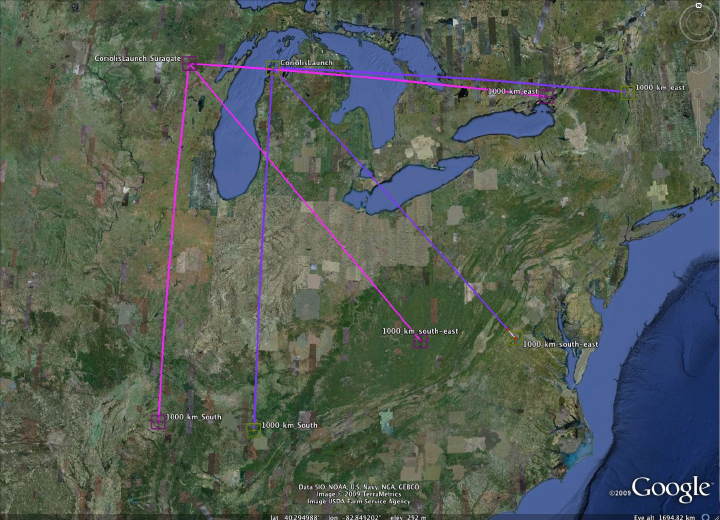
Here we will evaluate the effect on the cartesian coordinate system of azimuths and bearings when the Earth's spherical nature and rotation is considered. The Google Earth facility is employed to visualize the discussion, as shown in the graphic below. During our modeled 12 minute loft time, the Earth will rotate three (3) degrees of longitude from the west to the east [regardless of your location on the earth]. Therefore, the landing location of the ejecta will actually be three degrees westward of the initial "target".
When the ejecta is deposited at the eventual location, it will still bear the original flight azimuth/bearing. If those geometries are followed back along the trajectory, the will focus on a location three degrees west of the original launch location. Thus, we feel justified in applying the conceit that, from the perspective of the distal ejecta landing site, the inferred bearing would point back to a surrogate impact crater. The surrogate would offset on the global map by one degree of longitude westward for every four (4) minutes of loft time.
Please consider, also, that the loft time is a variable affected by both the launch velocity and its loft angle. A trajectory can be generated for a given landing location using shallow lofts (and short transit times) as well as higher loftings which would take longer to get to the same location.
Surrogate Crater Process using Google Earth Viewer
Heuristically, we initially chose to test fit against a set of ejecta sources across the norht-central US.
Using the model, we initially identified seven (7) placemarks [ LM_A through LM_G in the attached kml ] to use as proposed impact "sources". Using our surrogate crater conceit, we generated an additional seven placemarks offset to the west by 2 degrees longitude corresponding to a loft time of eight (8) minutes. Another set was created to test for loft times of 16 minutes, for a total of 21 placemarks, available in the kml.
For a select set of about 30 "fields" of ejecta, we created kml to depict the Carolina bay features, and identify their inferred orientation with a "Bearing Grid" overlay. A set of Great Circle GE paths were created from the field location back to each of the 21 LM-xxx positions identified above. The attached kml includes the details of the "Andrews" field, as well as a folder of its 21 Coriolis paths. Using the bearing grid overlay, several Coriolis paths which best fit the visualized orientation were selected. From that subset, an optimized path [ GC Andrews Optimum Coriolis Offset ] was generated that uses an average of the possible surrogate impact locations' latitude and longitude.
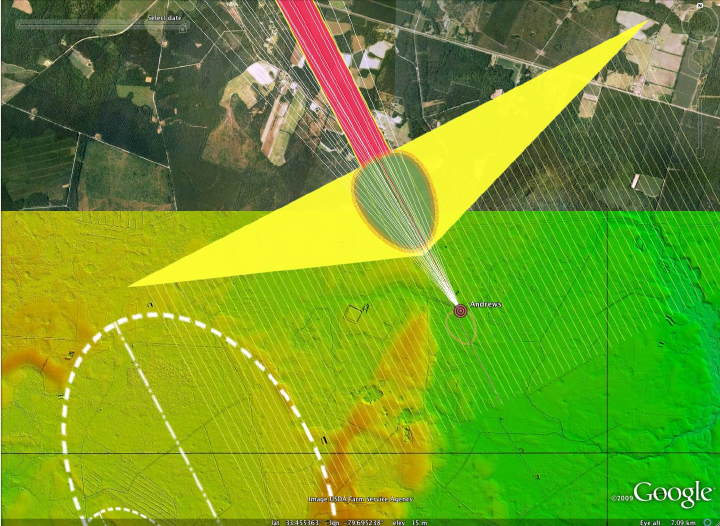
Chosing Best Great Circle Bearings from Coriolis Set
The Andrews Field kml includes outline overlays of multiple Carolina bays, DEM color-hinted elevation mappings in overlay form, and output from Global Mapper that displays the elevation profile along a sample path through the ejecta field. Note that the adjacent bays were created at several elevations. Our conjecture that the bays are surface features in a thin 1- 10 meter thick blanket overlaying the original terrain is supported by this evidence.
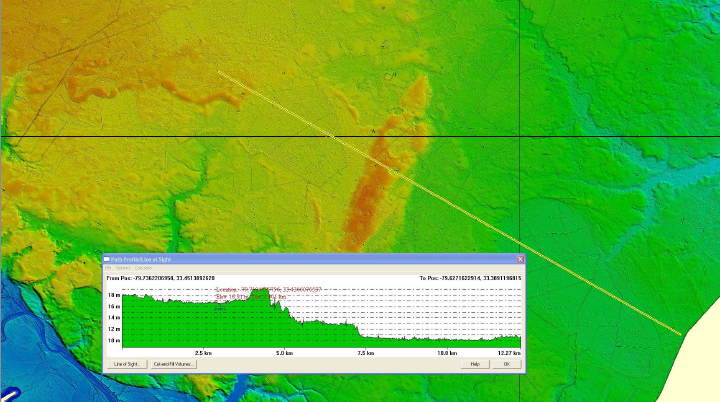
Profile View of the Andrews main bays - links to larger version
A set of inferred arrival bearings were computed for the 30+ fields, which were then used to generate a single point as a proposed impact location.The following Google Earth graphic is our computed trajectory path for this set.
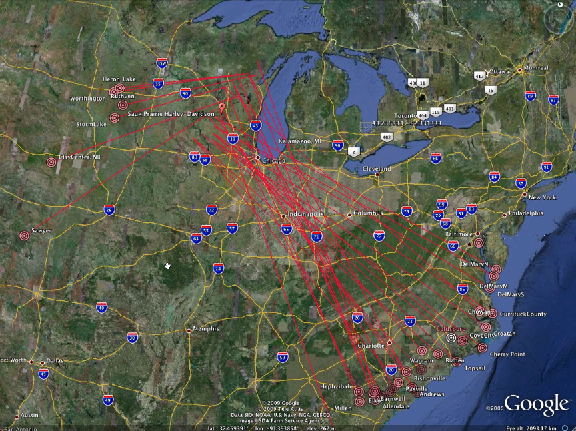
Carolina bay Primary Set Trajectory - linked to higher resolution image
An average of all optimum trajectories was used to generate a proposed single point locii for an imapact point. The location at 43.6259 North Latitude and 89.7043 west Longitude was computed. We extended the green line east along the indicated latitude to identify possible crater sources. This lead our search to the Saginaw Bay area.
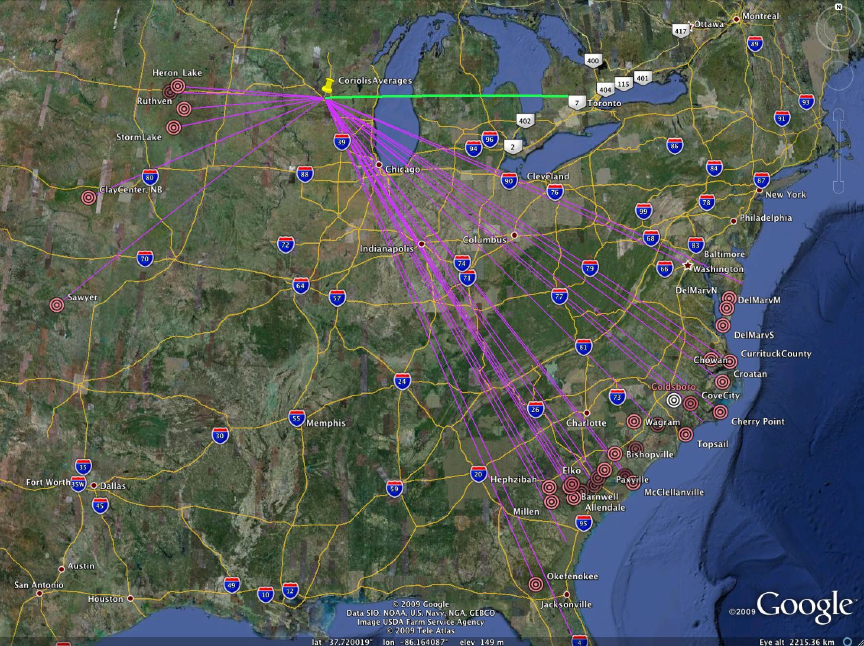
Carolina bay Optimized Average Trajectory - linked to higher resolution image
Following our conceit premise, we propose that the causal impact site was along the green line shown above, with the offset eastward driven by the loft time of the ejecta. For each 4 minutes of loft time, the earth will rotate one degree of latitude under the trajectory. As discussed in the Saginaw Bay section, we have moved our search for the impact crater to that area, which lies approximately 6 degrees east, which corresponds to a ~24 minute loft time.



